洪明洲教授部落格

等候理論(3)

等候模型除了推算等候發生的時間、人數外，最重要的是推算這些數值發生的機率。推算機率必須進入符號建構的數學運算領域，會嚇倒大家。是否可以不靠複雜數學，搞通等候機率？本篇內容正是。

由於Excel協助，我才有辦法設計出這套獨創的等候機率解說。在等候理論(2)，搞通了：（1）到達率、（2）服務率、（3）到達的時間間隔、（4）每次服務時間、（5）忙碌強度、（6）全程人數、（7）全程時間、（8）等候時間、（9）等候人數，9個等候專有名詞或等候值的意義、運算與關係，接下來，我們要建構對這些等候值出現機率的預測，以判定一個服務系統的優良品質與顧客服務水準，據以改良服務系統以提高服務水準。

上述9個數值中，服務率是企業最能控制的變數，但提升服務率常會提高營運成本，兩者必須加以平衡。忙碌強度是很好的決策指標，太高表示顧客必須等候，太低又是服務產能的閒置。所以應在表13調整數據，模擬各種情況，選取合宜的忙碌強度，以兼顧兩者。

進入主題之前，先建立3個觀念：

首先，前兩篇文章所敘述的數值，或者表13（重製為表14）所推算的（等候）時間、人數都是平均數值，如果從現場觀察，這些數值是隨機發生的，表13的數值是大數據的特徵值而已，協助我們掌握系統模型的特質。

其次，表14兩個直接輸入的數值：到達率與服務率，是（等候）時間、人數機率分配最重要的特徵值，換言之，當我們推算有3個人在等候的機率，會把這兩個數值其一（有時會同時）當作已知數，輸入公式求算（3個人在等候的）機率值。

最後，（等候、服務）人數、時間都呈指數機率分配。

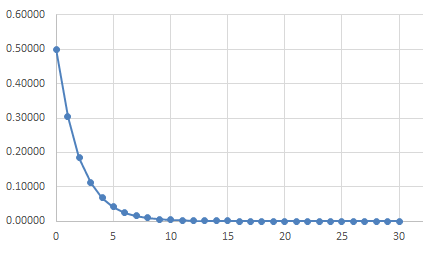
指數機率分配是一條像溜滑梯似地從左上方溜向右下方的曲線，溜滑梯曲線說明：某件事發生的個別機率都不同，第一次發生的機率很高，第二次發生的機率會急速下降，最後趨於平緩。意思是，第一次發生機率很高，第二次發生機率大幅下降，第三次降幅稍緩，第四次更緩，………以此類推，次數愈大，發生機率愈低，下降幅度愈小。

圖20

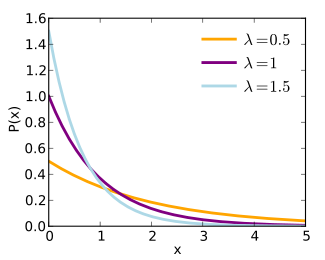
指數分配看似複雜，機率的計算卻非常簡單，基本公式是：把發生次數當成某一數值（作底）的指數。只要這一作底的數值小於1，次數愈大，機率就愈小。各位想像一個0.2（小於1）的機率數值，發生兩次，機率=0.04，發生三次，機率=0.008，……這就是指數分配。

有了指數分配的概念後，我們針對表13解答三組機率問題：（1）現場客人數目、（2）下一位客人等待時間、（3）多長時間沒有服務客人。第一題在求算人數的發生機率，後兩者求算時間（分鐘）的發生機率，每一組問題都取  0到30的次數求算機率。設計這三組問題目的在演練等候理論的機率運算公式，接下來再來解答不屬於指數分配的Poisson分配的機率問題，但先聲明，本篇文章還無法解說這些機率值在設計或改良服務系統的應用。

（一）現場客人數目

假設當現場只有一位服務人員，有多少客人正在現場？從沒人（0）、1人、2人……，到30人，機率各為何？

客人在現場，若非（一位）正在接受服務，就是（其餘都）在等待，本題的特徵值是忙碌強度，是到達率與服務率兩者相除，0.75=0.5/0.667，它與不忙碌比率加起來= 1，或者1-0.25=0.75。

1. 客人=0（沒客人），連一位在接受服務的客人都沒有，機率=0.25=不忙碌比率= 1-忙碌強度。

2. 客人=1，這位客人也許正在等待，也許正在接受服務，機率=0.25*0.75=不忙碌比率*忙碌強度。

3. 客人=2，兩位客人等於忙碌強度2次方（指數），機率=0.25*(0.75^2)=不忙碌比率*(忙碌強度^2)。

以此類推，每增加一位客人，忙碌強度都自乘一次，所以機率公式是：機率=不忙碌比率*(忙碌強度)^n，n是客人數。

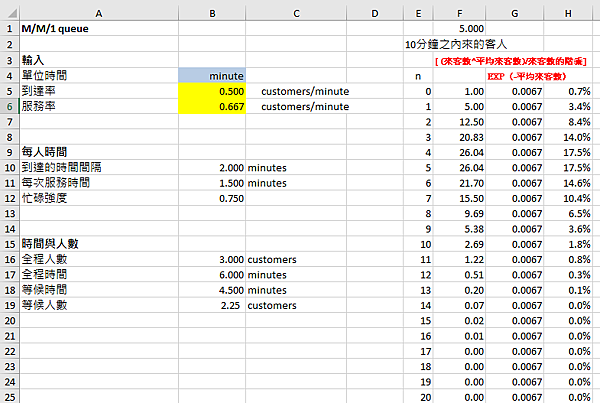
現場客人數目從n=0-30的機率列於Excel D欄位，E 欄位是它們個別的機率值，E5格輸入=(1-$B$12)*$B$12^D5 ，然後copy下來。若n=0（沒客人），上述公式(忙碌強度)^ 0=1)，所以機率=不忙碌比率。

表14

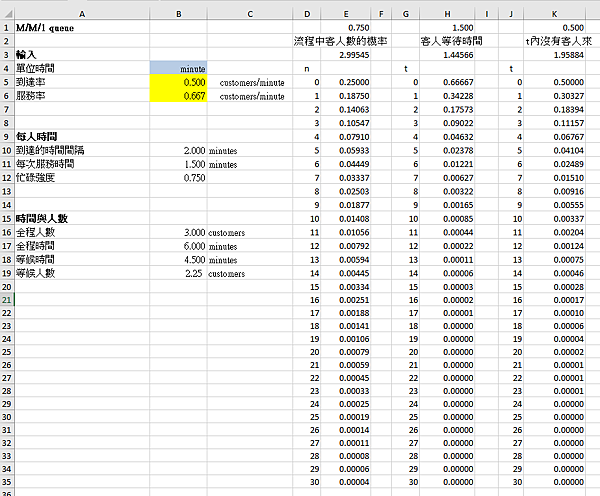
E3是用@SUMPRODUCT將兩個欄位數值相乘再加總的值，乃是這一機率分配的期望值，它接近於B16格的全程人數，也印證本文開頭說的：前兩篇文章所敘述的數值，或者表13所闡述的（等候）時間、人數都是平均數值（或特徵值）。

根據表14的DE欄位劃出本題的機率分配圖如下：

圖21

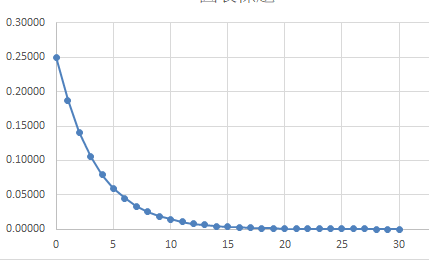
（二）下一位客人等待時間

推算下一位要接受服務客人的等待時間（t），它關連服務率（特徵值），它的機率公式是以等待時間為指數，底數是自然底數 e。

為何要以自然底數 e為底？它涉及複雜的數學推導，留給數學家去推導，您只要記住我教的公式就夠了。

自然底數 e 在Excel用EXP(t)表示，括弧內的t，表示自然底數 e的t次方，它幾乎是很多機率計算的基本值，亦即，很多機率公式都有這一成份，此一基本值乘上服務率（等待時間的特徵值），構成完整公式：

等待時間的機率 = 服務率*EXP（-服務率* 等待時間）

數學上，某值的負次方（指數），必然變成分數，數值一定小於1。Excel G欄位是從0到30的等候時間（分鐘），上述公式=$B$6*EXP(-$B$6*G6)輸入H6格，E欄列示下一位要接受服務客人要等待的機率。

如同上例，H3是用@SUMPRODUCT將GH兩個欄位數值相乘再加總的值，是這一機率分配的期望值，它接近B11格的每次服務時間。

圖21

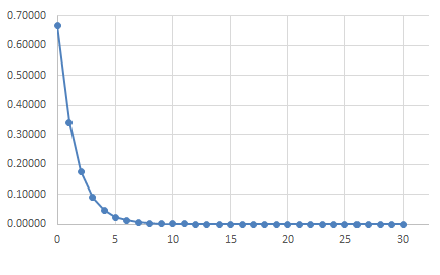
（三）多長時間沒有服務客人

當我們設計一套服務系統，我們會關心「多長時間沒有服務客人」，它的另一面是「多長時間顧客沒有到達」，1分鐘、2分鐘、3分鐘..........是顧客到達時間，所以它關連顧客的到達率（特徵值），它的機率公式是以到達時間為指數，底數是自然底數 e，公式為：

到達時間的機率 = 到達率*EXP（-到達率* 到達時間）

上述公式與前一題公式非常類似，它們都包含EXP(t)（基本值），指數若為（-服務率* 等待時間），EXP(t)前面一定是服務率，指數若為（-到達率* 等待時間），EXP(t)前面一定是到達率，兩個公式非常像，也很好記，表示它們有相同的推導過程與邏輯。

表14J欄位是從0到30的到達時間（分鐘），將=$B$5*EXP(-$B$5*J5)輸入K6格，copyK欄就是多長時間沒有服務客人到達時間的機率。如同上例，K3是用@SUMPRODUCT將JK兩個欄位數值相乘再加總，也是這一機率分配的期望值，它接近B10格的平均到達時間。

圖22

（四）多長時間內會來多少客人

除了上述3個機率問題外，依據表13/14的數據，我們會關心，10分鐘內會來多少客人的機率，它的10分鐘到達人數是每分鐘到達率的10倍，或者=0.5*10=5，平均來客數=5，來客人數呈Poisson 分配，它與指數分配有很密切的關係，演算公式中有一基本值：以平均來客數為指數，底數是自然底數 e，它的公式是這一基本值（前面）乘上(來客數^平均來客數)/來客數的階乘)：

來客數機率 =[ (平均來客數^來客數)/來客數的階乘]*EXP（-平均來客數）

表15

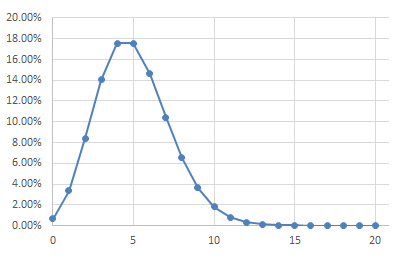
公式中的(平均來客數^來客數)/來客數的階乘)看似很複雜，但只要輸入Excel一次，copy，所有機率值就算出來了，如表15，基本值EXP（-平均來客數）=EXP(-5)=0.0067放在G欄位。公式的分子，平均來客數^來客數，是以平均來客數為底，來客數為指數，分母是來客數的階乘，若來客數=3，分母是：3*2*1=6，若來客數=4，分母是：4*3*2*1=24。來客數=0-3的機率值如下：

1. 10分鐘內客人=0，機率=EXP(-2)=0.7%

2. 10分鐘內客人=1，機率=[5/1]*EXP(-2)=3.4%

3. 10分鐘內客人=2，機率=[(5^2)/2]EXP(-2)=8.4%

4. 10分鐘內客人=3，機率=[(5^3)/6]EXP(-2)=14%

圖23

本文後記：

我設計的三組機率問題的求算，目的在提供讀者一套簡單的機率公式理解或記憶方法，簡單講，任何等候理論的機率分配，都從表13/14九個名詞定義出發，不斷輸入各種數據，包括使用Solver，加以模擬，才能強化對等候理論變數的理解，並徹底將上一篇文章搞懂。

表13的到達率、服務率，實務上，有許多相同的表達，例如關心某一段時間內客人的到達數，但這到達數不呈指數分配，它呈現的Poisson分配，更貼近現實，很多事物未必第一次發生後，下次發生的機率都會大減。

下一篇文章要進入.......多位服務人員(n>1)的等候情境。

有關指數機率分配的數學模型，強力推薦台大數學系翁秉仁教授的文章，Poisson 分配、指數分配與排隊理論，請上網查閱。